Tout ce que vous devez savoir sur les arbres de Merkle

Un arbre de Merkle ou arbre de hachage, nommé d’après le scientifique Ralph Merkle, est une structure de données basée sur le hachage qui est utilisée en cryptographie et en informatique.

Comme vous l’avez appris dans le cours 19 de la section Intermédiaire de la Bitpanda Academy, les fonctions de hachage sont utilisées pour uniformiser et sécuriser le contenu en longueur et pour identifier les transactions dans la blockchain.

Qu’est-ce qu’un arbre de Merkle ?

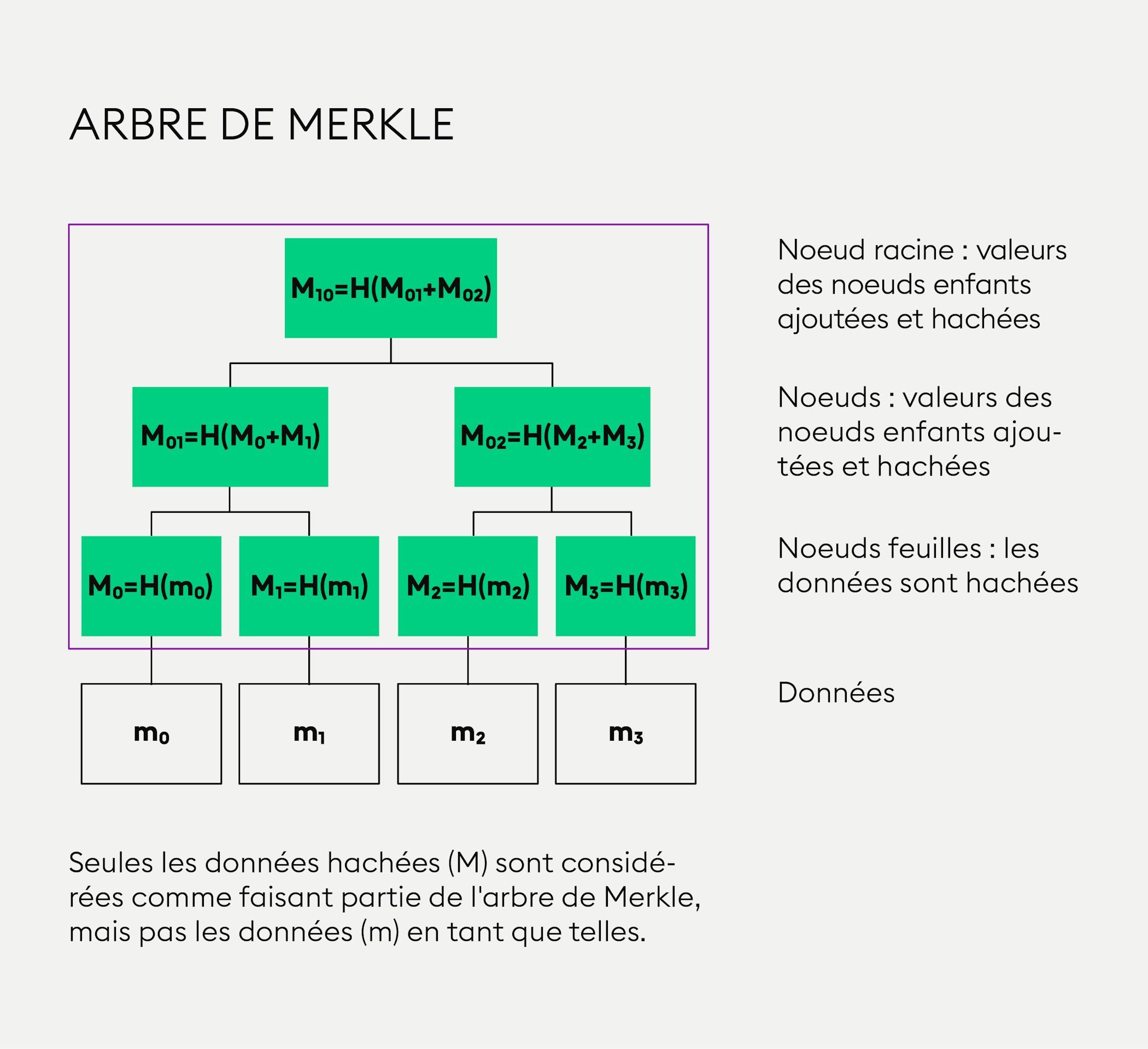
Dans le réseau Bitcoin, les arbres de Merkle sont utilisés pour la vérification des données. Cette méthode efficace consiste à utiliser des hachages au lieu d’un fichier d’informations complet. Un arbre de Merkle est un arbre de valeurs hachées, comme illustré dans l’image ci-dessous :

Les cases bleues dans la partie inférieure (« m0 », « m1 », « m2 » et « m3 ») représentent des données. Ces données « m » ne sont pas considérée comme faisant partie de l’arbre de Merkle. Si la valeur « m » dans ces cases est hachée, vous obtenez une valeur hachée « M », indiquée dans la case jaune au-dessus. 

Nœud racine et nœuds feuilles

Les cases jaunes dans l’infographie représentent les « nœuds feuilles » et correspondent aux données qui ont été hachées. Les deux valeurs « M0 » et  « M1 » sont jointes et hachées ensemble, comme l’indique le signe « + » dans la case gris foncé au-dessus. Il en résulte une autre valeur hachée contenant les « valeurs du nœud enfant ». Enfin, ces valeurs sont concaténées et hachées, donnant ainsi une seule « racine », également appelée « racine de Merkle ».

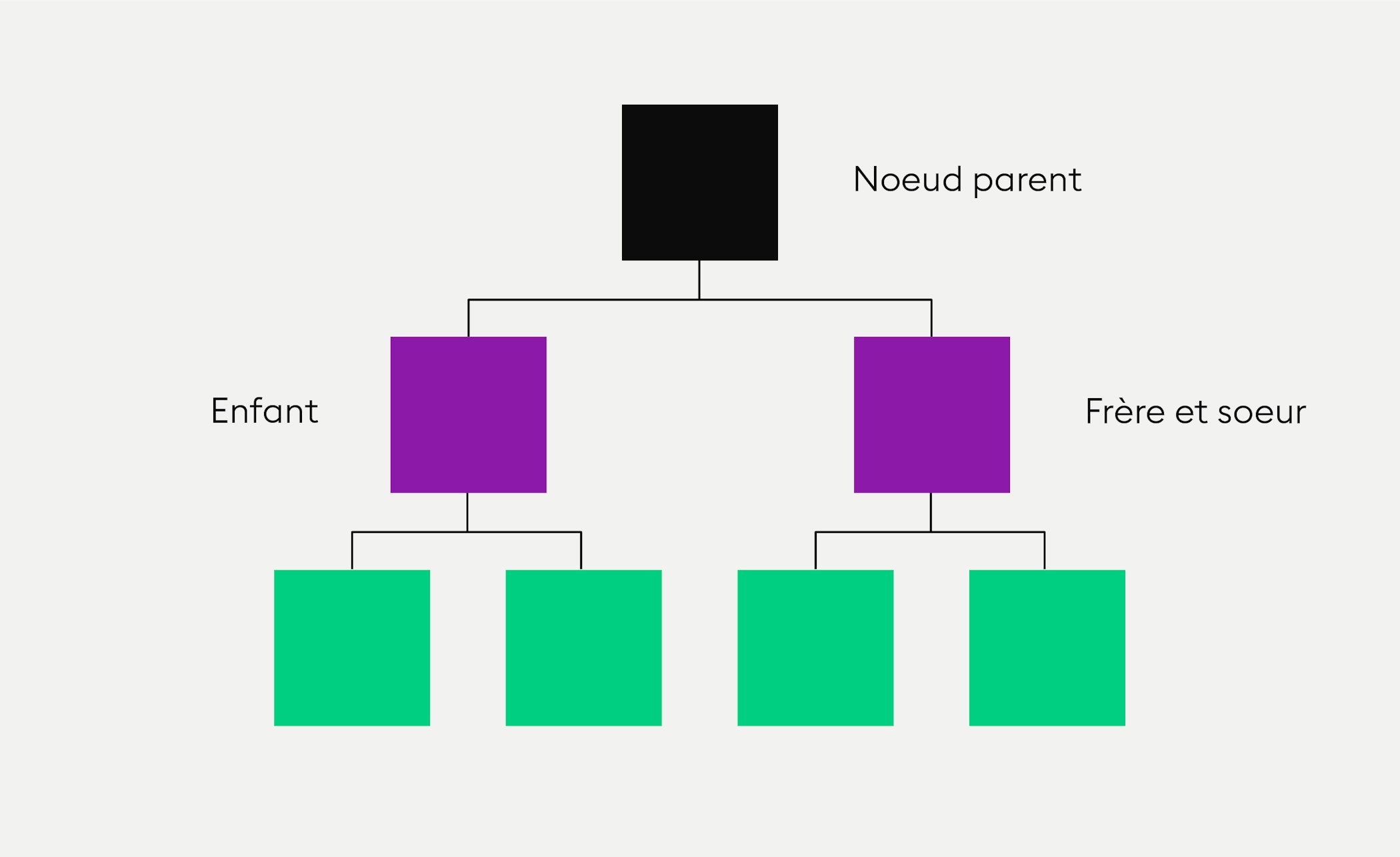
Les deux nœuds situés sous un nœud parent sont les « nœuds enfants » de ce nœud parent.

Le hachage de la racine est le hachage le plus élevé dans la structure de données hachées. Ce qui nous intéresse, c’est sa relation avec Bitcoin, où cette racine fait partie de l’en-tête du bloc. Elle détermine quelles transactions sont présentes.

Un arbre de Merkle utilise un type spécial de terminologie descriptive pour décrire la relation entre les nœuds et les niveaux de nœuds, tel qu’utilisé pendant le processus de vérification de paiement simplifiée (SPV). 

Un nœud contenant les valeurs des deux nœuds qui lui sont inférieurs est le « parent » de ces deux nœuds. Si chaque nœud a, au maximum, deux « nœuds enfants » ou « enfants », on parle d’un arbre de hachage binaire. 

Les deux nœuds situés sous un nœud parent sont les « nœuds enfants » de ce nœud parent. Les nœuds enfants côte à côte sont frère et sœur. Tous les nœuds inférieurs sans « enfants » sont appelés « nœuds feuilles » et sont au même niveau.

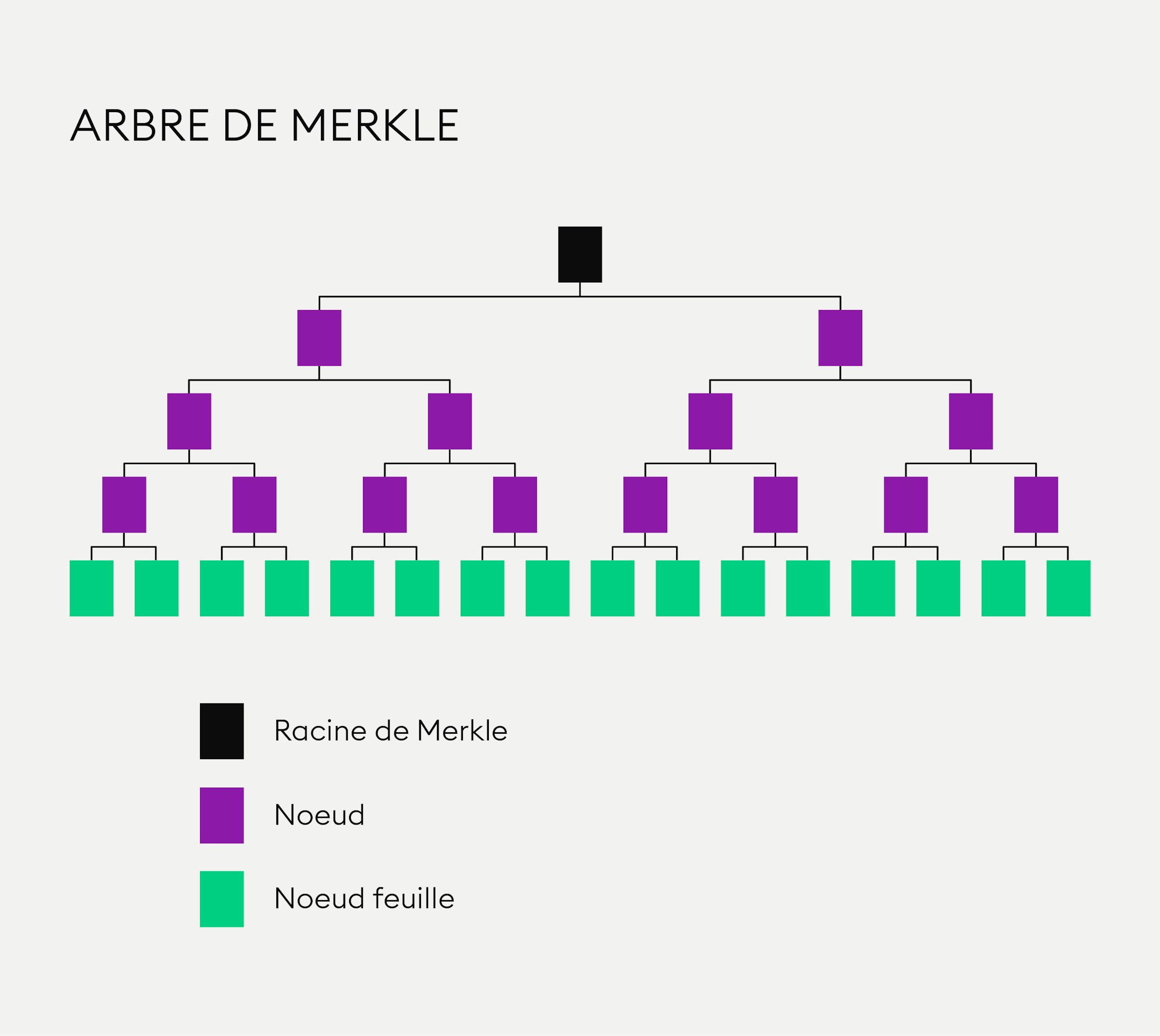
L’arbre de hachage est une structure arborescente dont chaque nœud feuille est un hachage d’un bloc de données. Les arbres de Merkle utilisent généralement une structure en arbre binaire, mais un niveau de sortie plus élevé est également possible. Dans la configuration d’un arbre de Merkle parfait, le nombre de feuilles est toujours 2n, la valeur « n » étant 1, 2, 3 etc. Chaque nœud a soit deux « nœuds enfants », soit aucun.

Comment les arbres de Merkle sont-ils utilisés dans la technologie blockchain et pourquoi ?

Dans le réseau Bitcoin, un arbre de Merkle résume toutes les transactions à l’intérieur d’un bloc en produisant une empreinte numérique de l’ensemble des transactions. De cette façon, un utilisateur est en mesure de vérifier si une transaction est incluse dans un bloc ou non.

Tous les nœuds de la structure arborescente de l’arbre de Merkle sont des représentations partielles des données hachées qui se trouvent en dessous d’eux.

Maintenant, vous vous demandez probablement pourquoi a-t-on besoin d’un arbre de hachage pour procéder à une telle vérification ? Ne pourrait-on pas hacher tous les messages (les données originales), placer les valeurs hachées dans une seule chaîne et obtenir la valeur du hachage racine de cette façon ? En quoi les arbres de Merkle facilitent-ils les choses ?

Question de confiance

Imaginez que les arbres Merkle n’existent pas. Au lieu de la racine de Merkle, nous stockerions le hachage de toutes les transactions de la blockchain dans l’en-tête du bloc. Pour vérifier une seule transaction, il faudrait donc télécharger les données de toutes les transactions. 

Les arbres de Merkle réduisent la quantité de données nécessaires à la vérification. Supposons que Suzie cherche à prouver à Pierre que la transaction « m6 » n’a pas été falsifiée. Pierre pourrait obtenir le hachage de la racine auprès d’une source de confiance et vérifier que c’est bien le cas. 

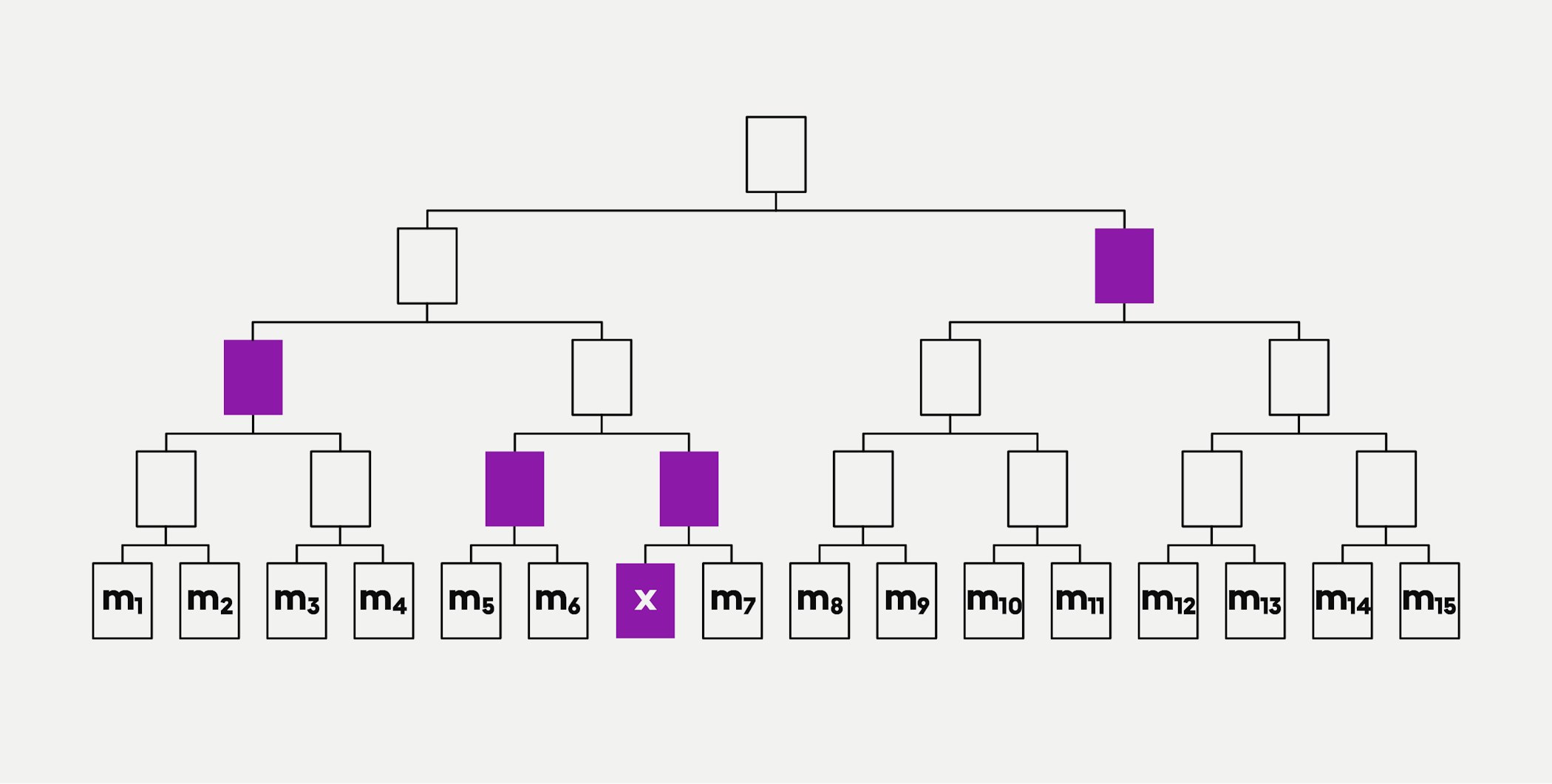
Si Suzie et Pierre procédaient sans arbre de Merkle, Suzie devrait fournir à Pierre toutes les transactions hachées pour prouver que « m6 » n’a pas été altérée. Un arbre de Merkle offre un moyen bien plus commode de le vérifier. Encore une fois, Pierre obtient la racine d’une source fiable. Cette fois, si Suzie veut prouver que « m6 » n’a pas été falsifiée, il lui suffit d’envoyer à Pierre le message et quatre valeurs hachées, comme indiqué en violet dans le schéma ci-dessous : 

Tous les nœuds de la structure arborescente de l’arbre de Merkle sont des représentations partielles des données hachées qui se trouvent en dessous d’eux. Chaque feuilles de l’arbre de Merkle est le hachage d’une transaction individuelle. 

Vérification des incohérences

Dans les réseaux distribués pair-à-pair tels que la blockchain Bitcoin, les mêmes données existent sur chaque ordinateur du réseau pair-à-pair. Chaque fois que la blockchain est modifiée par l’ajout d’une transaction, les changements sont reflétés simultanément sur chaque ordinateur du réseau tout entier. 

Pierre peut désormais reconstruire la partie pertinente de l’arbre de Merkle pour trouver la racine de Merkle. Il peut l’utiliser pour vérifier les valeurs hachées provenant d’une source non fiable. Si le hachage de la racine reconstruite correspond à la valeur de hachage de la racine provenant de la source de confiance, il peut les accepter. Il est plus facile et tout aussi sûr de recréer une partie d’un arbre de Merkle que de vérifier les données en les comparant à toutes les données hachées.

En résumé, l’utilisation d’un arbre de Merkle pour vérifier les incohérences accélère considérablement le processus de validation, car seuls les hachages et les fichiers qui ne sont pas encore complets sont envoyés sur le réseau, ce qui non seulement rend le processus plus pratique, mais utilise également beaucoup moins d’espace mémoire sur un ordinateur.